ASSA-PBN

ASSA-PBN 3.0: A Software Tool for Probabilistic Boolean Networks (PBNs)



The Tool Artefact for CMSB 2018 can be downloaded here

Description

ASSA-PBN is a software tool for modelling, simulation and analysis of probabilistic Boolean networks (PBNs), especially for large PBNs, which naturally arise in the domain of Systems Biology. ASSA-PBN provides several methods for analysing a PBN. This includes the basic steady-state computation, and the in-depth long-run influence and sensitivity computation, and parameter estimation of a PBN.

ASSA-PBN 3.0 supports context-sensitive PBN and attractor detection. Check more new Features.

Modules

The architecture of ASSA-PBN is shown in the figure below.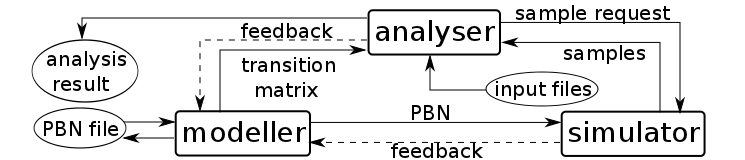



ASSA-PBN contains three major parts: modeller, simulator, and analyser. They interact with each other to provide a full support for PBN analysis. The modeller provides a simple way to construct a real-life biological system, e.g., gene regulatory network (GRN), into a PBN and supports visualisation and dynamically changing of a PBN. The simulator takes the PBN constructed in the modeller and performs simulation to produce samples. Simulation does not suffer from the state-space explosion problem even in terms of large PBNs since it is not based on the transition matrix. Based on the constructed model and generated samples, the analyser performs basic and in-depth analysis of the PBN. The analysis results can be used either to interpret the original system or to optimise the modelling of the system. The above figure shows the structure of ASSA-PBN. The analyser requires different input files depending on the analysis task. While simulator and analyser rely on modeller as input, the simulation and analysing results can be used to optimise modelling construction.

The basic analysis of a PBN refers to the computation of the steady-state probabilities. The analyser provides three different classes of methods for the computation of exact/approximate steady-state probabilities. The first class consists of two iterative methods for exact computation of the steady-state distributions: the Jacobi method and the Gauss-Seidel method. The second class consists of the perfect simulation algorithm [PW96] for sampling the steady-state of discrete-time Markov chains. It is based on the indigenous idea of the backward coupling scheme originally proposed by Propp and Wilson. The third class of methods consists of two statistical methods for the approximation of steady-state probabilities, i.e., 1) the Skart method [TWLS08] and 2) the two-state Markov chain approach [RL92]. The implemented numerical methods require the transition matrix of a PBN as input, which is supplied by the constructor; while the implemented statistical methods require simulated trajectories of the PBN as input, which are supplied by the simulator. Simulation is not based on the transition matrix, as a consequence it does not suffer from the state-space explosion problem even in terms of large PBNs.

Starting from version 1.0.4, ASSA-PBN supports multiple CPU-based parallel computation of steady-state probabilities [MPY15_2], significantly reducing the time cost for computing steady-state probabilities.

Starting from version 2.0.1, ASSA-PBN adds support for in-depth analysis a PBN. This includes parameter estimation of a PBN, long-run influence analysis of a PBN and long-run sensitivity analysis of a PBN.

Starting from version 2.0.2, ASSA-PBN supports multiple GPU-based parallel and structure-based parallel computation of steady-state probabilities; and high-level PBN definition format

Starting from version 3.0.0, ASSA-PBN supports context-sensitive PBNs and attractor detection.

The current version ASSA-PBN (version 3.0.0) provides the following functions. We hightlighted those newly added functions since version 2.0.4.

Download

In case you meet the followng error "Error: Could not find or load main class view.GUI.MainGUI" when loading the GUI, please make sure that you are using the standard Oracle Java (TM) SE Development Kit 8 (build 1.8.0_40-b25) and the folder you put the downloaded package has the executable permission. If this does not help, you can download the xassa file and replace the one in the bin folder using this.

Benchmark

See Benchmark here.

We have evaluated ASSA-PBN on a large number of randomly generated PBNs. ASSA-PBN aims to perform analysis of large PBNs. Therefore, our evaluation focuses on the two-state Markov chain approach and the Skart method, which are statistical methods, implemented for large PBNs.

Quickstart Guide

We show here how to build a real biological model and compute its steady-state probabilities in ASSA-PBN step by step. For the complete user guide, please download it here.

How to build a real biological model in ASSA-PBN?

In the newly released version, ASSA-PBN provides a high-level PBN definition format, which is much easier for users to define a PBN. The picture below gives the Boolean functions of a 3-nodes PBN which has a perturbation rate 0.1%. We will use it as an example to show how to build it in the high-level PBN definition format.

The example PBN contains three nodes x0, x1, and x2. Node x0 has one Boolean function and each of the other two nodes has two Boolean functions. The high-level PBN definition format description of this model is shown in the figure below. In this figure, a line starting with “//” indicates a comment line. The description contains four parts. The first part is the header, specifying the model type, the number of nodes and the perturbation rate. The second part is between the keywords nodeNames and endNodeNames. It lists the names of all nodes one by one. The order of the names determines the order of the nodes in ASSA-PBN. In ASSA-PBN, each node is assigned a unique non-negative integer as the ID of the node. Therefore, the order in fact determines the ID of the nodes in ASSA-PBN. A node name cannot start with a number and cannot contain the following characters: space, tab, & ! | ^ = : ( ) . The third part specifies the function and selection probability details for all the nodes one by one. The specification for each node starts with the keyword node, which is followed by the node name, and ends with the keyword endNode. Each line between the two keywords specify one Boolean function and its selection probability in the format of “probability : function”. The probabilities of a node will be normalised if they do not sum up to 1. The functions can be defined using parenthesis and the four different logical operations, i.e., logical and &; logical or | ; logical not !, and logical exclusive or ^. Note that the logical not operation is required to be surrounded by a pair of parenthesis, e.g., (!x2). The last part specifies the nodes that should not be perturbed. It starts with the keyword npNode and ends with endNpNode. If all the nodes should be perturbed, this part can be omitted.

ASSA-PBN allows constant functions. To define a constant true function, one need to use the format "probability : TRUE" (e.g., "1 : TRUE") while to define a constant false function, one need to use the format "probability : FALSE" (e.g., "1 : FALSE").

//The definition file always starts with the update modes:

//synchronous, rog, rmg, rmgrm, rmgro, rmgrorm, aro.

//For the detailed description of the updating modes, see the userguide.

type=synchronous

//specify number of nodes

n=3

//specify perturbation rate

perturbation=0.001

//We list the names of all nodes one by one below.

//Each line specifies one node name.

//The order of the names determines their orders in ASSA-PBN.

//A node name can not start with a number.

//The following characters are not allowed for a node name:

//space, tab, &!j^= : ():

nodeNames

x0

x1

x2

endNodeNames

//We list the functions for each node one by one.

//Each line contains 1 Boolean function.

//It starts with a positive number denoting the selection

//probability. The double number is separated with the remaining part

//using ":". "0" is not allowed for probability. If the probabilities

//for a node do not sum up to 1, they will be normalised.

node x0

1.0 : x0&x1

endNode

node x1

0.3 : (!x2)&(x1jx0)

0.7 : (!x0)&x1&x2

endNode

node x2

0.4 : (!x0)&x1

0.6 : x0&x1&(!x2)

endNode

npNode

x2

endNpNode

Download: example-1.pbn

How to define the states, of which the steady-state probability is to be computed?

ASSA-PBN can read a property specification file, which defines the set of states whose steady-state probability is to be computed. The format of the property specication file is very simple. It contains only three lines. The first line specifies how the nodes are refereed in the file. The nodes can be refereed either by node name of by node ID. To refer by node name, put "refer=name" in the first line; and to refer by node ID, put "refer=ID". The second line specify those names/IDs of the nodes, whose values should be 1 (active); while the last line specifies those names/IDs of the nodes, whose values should be 0 (inactive). The indices in the same line are separated with a blank. Below is an example of specifying properties with node name:

refer=name
x0 x2
x1
Download: property-1-name.pro
In this example, we are interested in those states that nodes x0 and x2 are active and node x1 is inactive. In fact, there is only one interested state, i.e., 101.

Assume that we are interested in those states that node 1 is active. To define those states, the node ID 1 should be put in the first line and no node ID should be but in the second line. In this case, we put -1 in the second line, indicating that those inactive nodes are not relevant in this property. See below for the corresponding property definition file, which defines a set of 4 states, including 010, 011, 110, 111.

refer=ID
1
-1
Download: property-2.pro

How to load a model in the GUI?

Starting from version 2.0, ASSA-PBN provideds a GUI user convenience. Normally, the first step of analysing a PBN in ASSA-PBN is to load the PBN model. Double click "xassa" to launch the main interface of ASSA-PBN. Select the menu option "Model | Load" and select the PBN file to load the model.

How can I compute the steady-state probability of a PBN in ASSA-PBN?

After constructing the PBN definition file and the property definition file, one can easily compute the steady-state probability with one command line in ASSA-PBN. For example, to compute the steady-state probability for a PBN defined in "example-1.pbn" and the states defined in "property-1.pro" with the two-state Markov chain approach, just type the following command in a terminal:

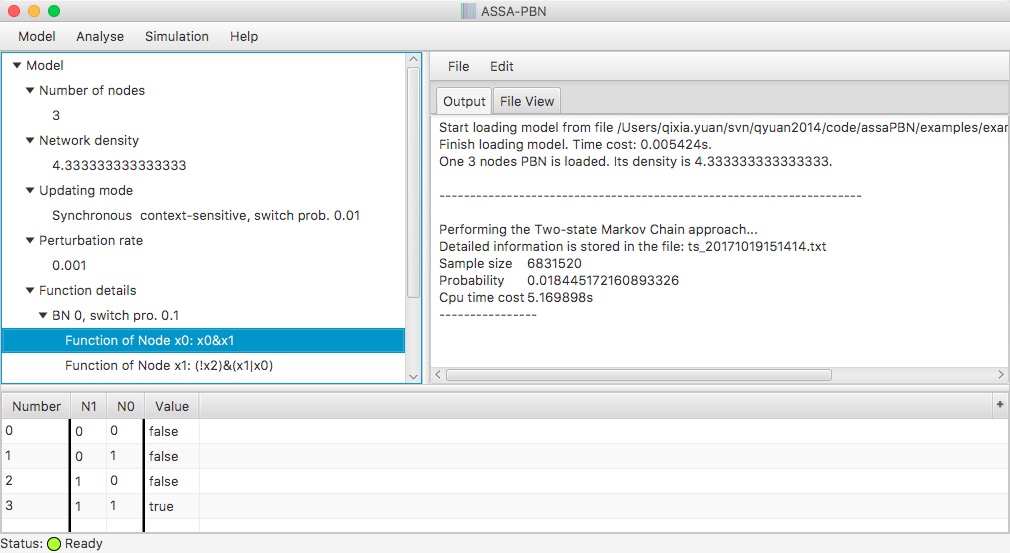
./assa -ts example-1.pbn 0.001 0.95 property-1.pro
0.001 is the precision and 0.95 is the confidence level.

Alternatively, the above operation can be done in the GUI of ASSA-PBN easily as well. After loading the model, select the menu option "Analyse | Steady State Probability | Statistical | Two State Markov Chain". In the pop-up window, set precision and confidence level, select the property file "property-1.pro", and click compute. The result is then shown in the top right panel. See the figure below for a screenshot.



Requirements

1. Platform: x86 compatible 32 bit or 64 bit processor;

2. Operating system: Windows, Linux and Mac OSX (10.4 and above);

3. Required environment: Oracle Java (TM) SE Development Kit 8 (build 1.8.0_40-b25) or later;

4. Required compilers (for attractor detection): flex 2.5.4 or higher, GNU bison 2.3 or higher, GNU g++ 4.0.1 or higher; Cygwin 1.5.25-14 or higher (Windows platform only); NVIDIA's CUDA Compiler (for GPU computation only).

References

Security and Trust of Software Systems
Belval Campus, Maison du Nombre (3rd floor), 6 avenue de la Fonte, L-4364 Esch-sur-Alzette, Luxembourg