Benchmarks of ASSA-PBN

Evaluation results of the GPU-accelerated steady-state computation can be downloaded here.

Benchmarks of ASSA-PBN versions 2.0.*

The benchmarks for version 2.0.* aims for the evaluation of parallel computing. There are three types of parallel computation methods, i.e., multiple CPU based parallelisation; multiple GPU based parallelisation; and structure-based parallelisation. We evaluate them on random networks and real biological networks one by one.

The evaluation of multiple CPU based parallelisation method is evaluated on 18 random networks. The detailed description of multiple CPU based parallelisation can be found in [MPY16]. We randomly generate 18 different PBNs with node numbers from the set {80, 100, 200, 500, 1000, 2000} using ASSA-PBN. For each node number, 3 PBNs are generated. We use the mulitple CPU based method to compute the steady-state probabilities of those 18 networks and compare the time cost of that using the sequential method. Due to the large size of dense networks, we only provide the sparse networks used in this evaluation here.

We evaluate the simulation speed of the structure-based parallelisation method using thousands of random networks. The evaluation results can be found here. We refer to [MPY16_2] for description of the details of the structure-based parallelisation method.

The GPU based parallelisation method applies the same algorithm as the CPU based parallelisation method. The difference is that GPU based method makes use of multiple GPU cores to perform parallelisation. In order to maximize the computation ability of a GPU, we optimize the data structure and the way we arrange data in a GPU. We evaluated our GPU implementation on 380 randomly generated networks. The results can be downloaded here.

We also evaluated the above three methods on a real-life biological system, i.e., the apoptosis network containing 96 nodes. The evaluation results are shown here. The apoptosis network is available here

Benchmarks of ASSA-PBN versions 1.0.*

We have evaluated ASSA-PBN on a large number of randomly generated PBNs. ASSA-PBN aims to perform analysis of large PBNs. Therefore, our evaluation focuses on the two-state Markov chain approach and the Skart method, which are statistical methods, implemented for large PBNs.

We generated 882 different random PBNs using our tool ASSA-PBN. See the user guide on how to generate a random PBN in ASSA-PBN. Those PBNs were generated with different node numbers, which were selected among the set {15, 30, 80, 100, 150, 200, 300, 400, 500, 1000, 2000}. We divided those PBNs into three different classes based on their densities: dense models with density 150-300, sparse models with density around 10, and in-between models with density 50-100. The density D in the output information is computed with the following formula:

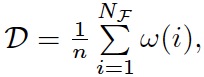
where n is the number of nodes in the PBN, N_F is the total number of functions in the PBN, ω(i) is the number of parents node for the ith function. We set ε to 10^-10 for the two-state Markov chain approach and the confidence level s to 0.95 for both methods. The precision r is selected among the set {10^-2, 5*10^-3, 10^-3, 5*10^-4, 10^-4, 5*10^-5, 1*10^-5, 5*10^-6, 1*10^-6}.

We then performed the two-state Markov chain approach and the Skart method using ASSA-PBN on those generated models. The experiment were performed on a HPC cluster, with CPU speed ranging between 2.2GHz and 3.07GHz. The initial and maximal Java virtual manchine heap size were set to 503MB and 7.86GB by default. We collected the estimated steady-state probabilities computed by the two methods, their trajectory sizes, and their CPU time costs as the experimental results. The results can be downloaded here. The experimental results show that our tool ASSA-PBN is able to handle large PBNs with a few thousand number of nodes with both the two-state Markov chain apporach and the Skart method.

We selected 5596 valid results (precision being smaller than the probability), and made further comparison on the performance of the two methods. The details of the comparison were descibed in [MPY15]. We provided the detailed experiemental data here. Due to the fact that the model file usually gets too big when the node number is large (more than hundreds of nodes), we give here only 10 sparse models with node number up to 1,000, 4 in-between models with node number up to 100 as well as the property specification used in the test. For the other models we used in the evaluation, please contact qixia.yuan#uni.lu (replace # with @).

References

[PW96] Propp, J.G., Wilson, D.B.: Exact sampling with coupled markov chains and applications to statistical mechanics. Random Structures & Algorithms 9(1) (1996) 223–252
[TWLS08] Tafazzoli, A., Wilson, J., Lada, E., Steiger, N.: Skart: A skewness- and autoregression-adjusted batch-means procedure for simulation analysis. In: Proc. of the 2008 Winter Simulation Conference. (2008) 387–395
[RL92] Raftery, A., Lewis, S.: How many iterations in the Gibbs sampler? Bayesian Statistics 4 (1992) 763–773
[TMPTS14] Trairatphisan, P., Mizera, A., Pang, J., Tantar, A.A., Sauter, T.: optPBN: An optimisation toolbox for probabilistic boolean networks. PLOS ONE 9(7) (2014) e98001
[MPY15] Mizera A., Pang J., Yuan Q.: Reviving the two-state Markov chain approach (technical report). Available online at http://arxiv.org/abs/1501.01779 (2015)
[MPY16] Mizera, A., Pang, J., Yuan, Q.: Parallel approximate steady-state analysis of large probabilistic boolean networks. In Proc. 31st ACM Symposium on Applied Computing - SAC'16, pp.1-8. ©ACM Press, 2016.
[MPY16_2] Mizera, A., Pang, J., Yuan, Q.: Fast simulation of Probabilistic Boolean Networks (technical report). Available online at http://arxiv.org/abs/1605.00854 (2016)